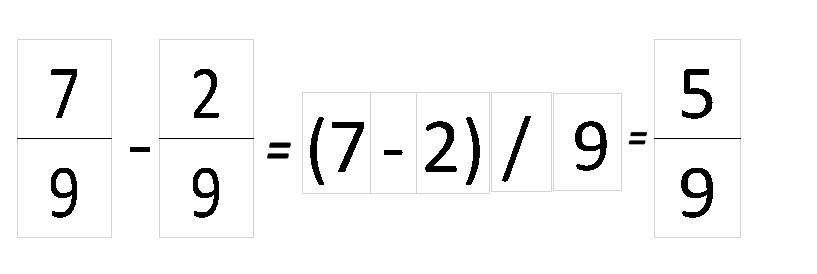Каждый школьник, перешагнув первую школьную ступеньку из начальной школы, начинает изучать новый для него материал – дроби. Не смотря на то, что на первый взгляд тема кажется не простой, на самом деле ничего сложного в ней нет, мы постарались ее объяснить доступным языком. Опытные педагоги рекомендуют объяснять ребенку тему дробей и в более раннем возрасте, так как, в повседневной жизни мы постоянно сталкиваемся с дроблением, делением предметов на доли – режем арбуз, торт, пиццу на определенное количество частей, каждая из которых будет частью целого, что и можно записать в виде дроби.
Обыкновенные дроби 5 класс объяснение темы
Если ваш ребенок не понимает тему дробей, очень важно объяснить ему так же, как объясняют в классе и учитывать требования учителя. Детям самим не так просто самостоятельно понять все действия с дробями, задача родителей помочь и привести примеры, которые встречаются каждый день в повседневной жизни. Дайте ребенку шоколадку и попросите отломить от нее часть: целая – это единица, половина – одна вторая, а если плитку разломить на три части, это будет одна треть.
Чтобы лучше понять что такое дробь, нужно запомнить, что это значит – дробить. Когда мы режем торт, каждый кусок будет частью целого торта или очищаем мандарин, каждая долька – это часть целого мандарина. В обоих случаях, это доли целого. Не сложно привести и другие примеры, каждый день мы что-то режем, отделяем.
Арбуз разрезали на 6 частей, каждая часть (доля), это одна шестая от целого плода.

На этой картинке два мандарина. В одном оказалось 6 долек, в другом – 9.

На картинке ниже наглядно видно, как прописываются дроби:

Вот еще пример, желтый круг разрезали на 2 части, это будет одна вторая доли (1/2), зеленый – на 3 (1/3), синий – на 4 (1/4).

Итак, что нужно знать ребенку о дробях?

Чем на меньшее число поделено что-то целое, тем долей больше, а если на большее число, значит они меньше.
Виды обыкновенных дробей
Доли в математике обозначают дробями, называются они – обыкновенные. Для записи используют горизонтальную (-) или наклонную черту (/), например:

Черта между цифрами означает знак деления и может быть заменен на две точки (:) !

Если пиццу разрезать на 6 кусков, а съесть только 2, то дробь вида 2/6 будет означать, что съели 2 куска из 6. В этом случае число “2” будет располагаться над чертой и называется оно “числитель” , а число “6” (под чертой) – “знаменатель”, т.е., съели две шестых пиццы.

Далее, нужно понять, сколько кусочков осталось: 6-2=4. Осталось 4 куска, в этом случае дробь выглядит так – 4/6 четыре шестых.
Обыкновенная дробь правильная неправильная
Еще дроби бывают правильными, например те, которые имеют такой вид – 2/8 и неправильными – 8/2 или 8/8. Возьмем неправильную дробь 41/5, читать ее следует так – восемь целых, одна пятая: 8 1/5. Это число называют смешанным, так как в нем отделяются целая часть и дробная. Другими словами мы наглядно видим сколько взяли целых тортов и сколько его частей. Чтобы ребенок осмысленно сокращал дроби, нужно показать ему это на практике и тогда он не будет ошибаться, сокращая дроби.
Для понимания: неправильная дробь трансформируется в целое число, сначала числитель делиться на знаменатель, в результате получается целое число (записывается, как целая часть) и остаток (записывается над чертой) в числитель. Знаменатель, при этом, не меняется.
К неправильным относят и те дроби, числитель и знаменатель которых, имеют одинаковое число, а при делении получается единица – 2/2, 3/3, 4/4 и т.д. Т.е., было взято столько кусков торта, на сколько его поделили.
Наглядно вы можете посмотреть на картинке:

Умножение и деление обыкновенных дробей
Прежде чем приступить к изучению вопроса об умножении и делении дробей, вспомним, что такое натуральные числа? А это те, которые начинаются с единицы – 1 и продолжаться могут до бесконечности. Но, к ним относятся только положительные числа, т.е, со знаком “+”. Числа: -1; -2; -3; -4; -5 и т.д., натуральными не являются.
Для того, чтобы совершить действие умножения, нужно умножить числитель одной дроби на числитель другой и, соответственно, перемножить знаменатели. Что у нас получается? В результате вычисления (умножения) мы получаем дробь с числителем, который равен произведению числителей в дробях, и со знаменателем, равным произведению в дробях знаменателей.

Пример:
Умножается число 3 на число 7 (числители). Умножаются знаменатель 5 на знаменатель 10. Записать данное действие можно двумя способами, это вы видите на картинке.

Пример умножения целого числа и дроби:
Целое число (2) записывается в виде дроби (2/1), в которой знаменателем будет единица (1).
![]()

Если нужно произвести деление дробей, поступают следующим образом: умножают первую дробь на перевернутую вторую.

Для простоты восприятия воспользуемся правилом сокращения: делим делитель и знаменатель на одинаковое число, например, дробь 21/63 выглядит не очень хорошо для восприятия, гораздо понятнее будет так – 1/3.

Делим смешанные числа:
Сначала их нужно представить неправильными дробями, затем, разделить друг на друга, вот, что получилось:


Пример:

Обыкновенные дроби сложение вычитание
Правила сложения
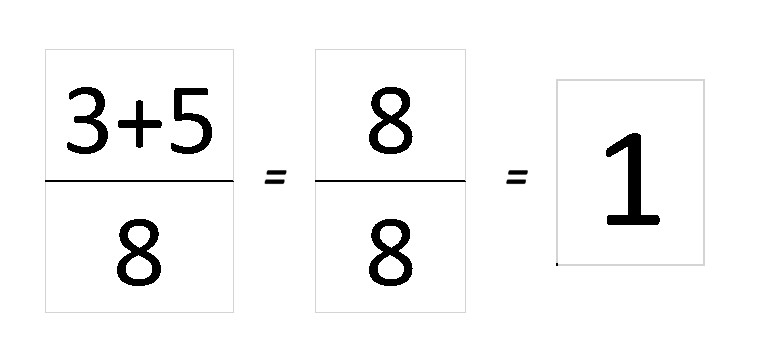
Начнем с дробей, у которых одинаковые знаменатели, это самое простое вычисление – высчитывается сумма только числителей – тех чисел, которые находятся над черточкой.
Например:

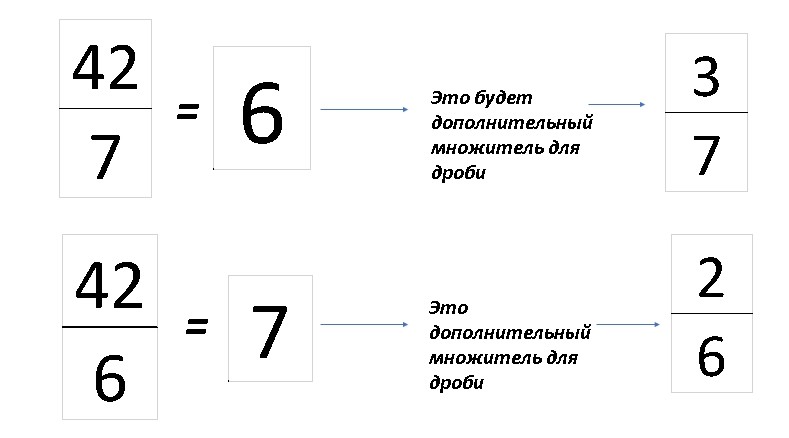
Немного сложней выполнить действие сложения, если знаменатели разные. В этом случае необходимо сначала:

Пример:
Далее:
Затем, каждую часть дроби, знаменатель и числитель, нужно умножить на свой множитель, который мы определили:
 Далее производим сложение дробей:
Далее производим сложение дробей:

Правила вычитания
Действие производится аналогичным образом, если у дроби знаменатели одинаковые, необходимо найти разность числителей.
Если у дроби знаменатели разные, Так же, как и при сложении, находим наименьшее кратное число.
 Сравнение дробей 5 класс
Сравнение дробей 5 класс
Прежде всего необходимо обратить внимание на их знаменатели, если они одинаковые, меньше будет та, чей числитель больше.
Пример:

А если числительные одинаковые, меньше та, чей знаменатель больше.
Пример:

Сложнее обстоит дело, если знаменатели разные. В этом случае сначала определяем общий знаменатель (под чертой) и приводим к нему обе дроби.
Пример:

Далее получаем:

Сравниваем:

Запомните!

P.S. Итак, мы рассмотрели одну из тем по математики для 5 класса. Ее необходимо знать, чтобы ребенок смог двигаться дальше и изучать более сложный материал.
Для лучшего понимания покажите ребенку видео.